ICS3U Learning To Problem Solve With Python Part 1
ICS3U Learning Goals
In this ICS3U lesson you will be learning how to
- Write pseudo code using the input-processing-output method of problem solving.
- Add documentation to a python program
- Evaluate the solutions to more complex problems
Problem Solving in Computer Science
Generally in ICS3U we solve a lot of problems in computer science using an algorithm. (A series of steps that lead you to the correct answer) The INPUT – PROCESSING – OUTPUT model of problem solving generally works pretty well in this course for solving straightforward computational problems
- Input – Lists the data needed to be stored or entered from the user
- Processing – The logic / math, steps needed to solve the problem
- Output – Lists what is required to be displayed on the screen when the program is running or finished
ICS3U Problem Solving Example
ICS3U Paint Store Question
Let’s say you wanted to write a program that helps a user determine how many cans of pain they will need to pain the walls and what the total cost will end up being. Let’s assume that each can of paint will cover 4m2 of wall space and will cost $17.50 per m2. There will be tax on the final price, so assuming we are in Ontario, there is a 13% HST.
Important Information From the Video
Input
The following information will be needed from the user in order to solve the problem
- the length of the wall -> Decimal number
- the height of the wall -> Decimal number
- the number of coats of paint needed -> Integer
Processing
The total area to be painted is the area of the wall multiplied by the number of coats of paint
$$ Area = (length)(width) (coats) $$
$$ Buckets = \frac {Area}{4} $$
This value must be rounded up because you can’t buy a partial bucket.
Since each bucket of paint costs $17.50, we can calculate the total cost as follows
$$ subtotal = (Buckets) ($17.50) $$
$$ cost = (subtotal)(1.13)$$
Output
The important information the user needs to see after the app is finished processing is the number of buckets of paint that need to be bought and the total after tax cost
The Solution
It is standard programming practice to document your code to make it clear to others what the “main” parts of the code are doing. Comments are non executed lines of code. You can add a comment by starting the line with an #
import math
#Get input from the user
length = float(input("Enter the length of the wall: "))
height = float(input("Enter the height of the wall: "))
coats = int(input("How many coats will you paint? "))
#Calculate the amount of paint needed
area = length * height * coats
buckets = math.ceil(area / 4)
#Calculate the cost of the paint
subTotal = buckets * 17.50
total = subTotal * 1.13
#Output the results
print("\nReceipt:")
print("You will need",buckets,"buckets of paint")
print("Final Price: $", round(total,2))
The Evaluation
To complete the process its time to evaluate the code to see if it is giving the results that are expected. Generally you should run your program several times with a range of data where you can verify if the program is working properly

In this case it would be best to get out a calculator and check. If the results are not as expected, you need to go back and think about where you made a mistake
ICS3U Problem Solving Example
ICS3U Quadratic Functions Questions
You have been assigned the task of helping a grade 10 math class with converted the factored form of a quadratic to its standard form as well as calculating the coordinates of the vertex of that quadratic.
Important Information from the Video
Input
Here are some quadratics in factored form:
$$ y = (2x+5)(3x+7) $$
$$ y = (5x-3)(4x-9) $$
In general, it looks like there are 4 pieces of information in each factored quadratic. They are represented by the variables a, b, c, d in the equation below. Those values are all integers.
$$ y = (ax+b)(cx+d) $$
It would be appropriate at this point in the course to ask the user to enter the individual values for a,b,c,d separately, and not enter the entire quadratic function. We don’t yet know how to parse an input like that to pick out the appropriate information.
Processing
You need to change the factored form of the quadratic into the standard form. That is done by expanding the factored form. (Remember FOIL). For example, the two examples above would end up as follows:
Example1:
$$ y = (2x+5)(3x+7) $$
$$ y = (2)(3)x^{2} + (2)(7)x + (5)(3)x + (5)(7) $$
$$ y = 6x^{2} + 29x + 35 $$
Example 2:
$$ y = (5x-3)(4x-9) $$
$$ y = (5)(4)x^{2} + (5)(-9)x + (-3)(4)x + (-3)(-9) $$
$$ y = 20x^{2} - 57x + 27 $$
The key is now looking for a pattern and comparing that to the general quadratic with only variables inside it.
$$ y = (ax+b)(cx+d) $$
$$ y = (a)(c)x^{2} + (a)(d)x + (b)(c)x + (b)(d) $$
$$ y = acx^{2} +(ad+bc)x + bd $$
The standard form of the quadratic has 3 numbers you need to calculate.
$$ y = Ax^{2} + Bx + C $$
$$ A = ac $$
$$ B = ad + bc $$
$$ C = bd $$
Now that you have figured out how to get the standard form, you can start to figure out the vertex. The x coordinate of the vertex is in the middle of the zeros of the quadratic. For example in the first example. There are two zeros
$$ zero1 = \frac{-5}{2} = -2.5 $$
$$ zero2 = \frac{-7}{3} = -2.333 $$
$$ xvertex = \frac{-2.5+-2.33}{2} = -2.416 $$
Now the y value of the vertex can be found by plugging in the x vertex value back into the original quadratic.
$$ y = (2(-2.416)+5)(3(-2.416)+7) = -0.0417 $$
If you generalize that to the a,b,c,d variables then
$$ zero1 = \frac{-a}{b} $$
$$ zero2 = \frac{-c}{d} $$
$$ xvertex = \frac{zero1+zero2}{2} $$
$$ y = (a(xvertex)+b)(c(xvertex)+d) $$
Output
The output needs to be the A, B, C values of the standard form of the quadratic. It should be displayed as a quadratic and not just the 3 values.
The vertex should be displayed to look like an ordered pair since it is a point on the graph.
The Solution
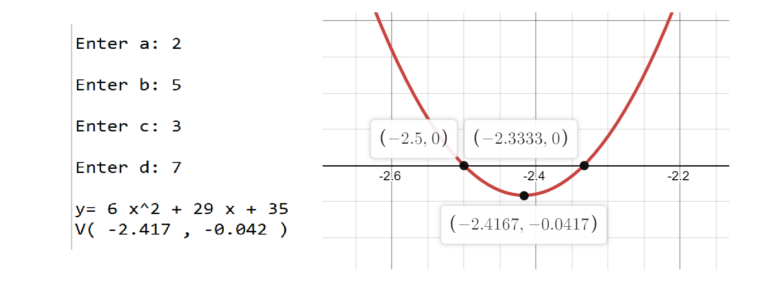
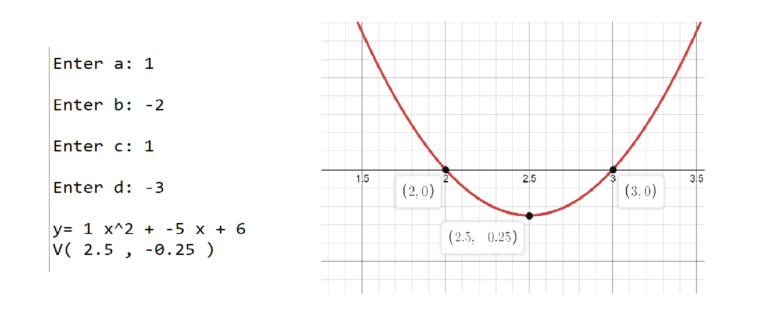
#Get the inputs from the keyboard
a = int(input("Enter a: "))
b = int(input("Enter b: "))
c = int(input("Enter c: "))
d = int(input("Enter d: "))
#Calculate A,B,C
A = a*c
B = a*d + b*c
C = b*d
#Calculate the x value of the vertex
x1 = -b/a
x2 = -d/c
x = (x1+x2)/2
#Calculate the y value of the vertex
y = (a*x + b)*(c*x + d)
#Display the answers
print("\ny=",A,"x^2 +",B,"x +",C)
print("V(",round(x,3),",",round(y,3),")")
The Evaluation
In this case it might be appropriate to check the solution with a graphing calculator
ICS3U Coding Questions
Try to code the following ICS3U questions using an IDE of your choice (Spyder, IDLE, Pycharm, etc). You will save those files on your computer for future reference.
Make sure you are completing the Input-Processing-Output Problem Solving Process before you start your code. Clearly evaluate the solution when finished.
Each question has:
- A video of your teacher live coding and explaining the solution
- The final code used in the video.
Try your best to solve the problems yourself without looking at the solutions.
Make sure you test your programs with multiple different inputs to ensure it is functioning properly.
ICS3U Practice Question
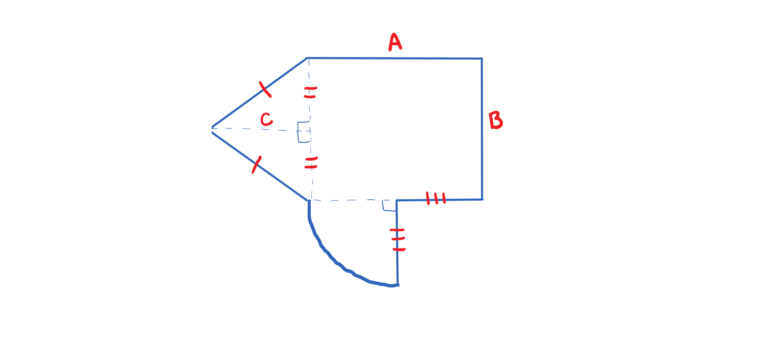
Name Your File : “ICS3UweirdGeometry.py”
Consider the shape below and assume that the values A, B, C are entered from the keyboard.
Display the area, perimeter, and 3 interior angles of the triangle. Round all answers to 2 decimal places.
import math
#Get input from the keyboard
A = int(input("Enter A: "))
B = int(input("Enter B: "))
C = int(input("Enter C: "))
#Find the hypotenuse of the triangle
s = math.sqrt(math.pow(B/2,2)+math.pow(C,2))
#Find the area
area = A*B + 1/2*B*C + 1/4*3.14*math.pow(A/2,2)
#Find the perimeter
perimeter = A + B + A + 1/4*2*3.14*A/2 + 2*s
#Find the angles
theta1 = math.degrees(math.atan(C/(B/2)))
theta2 = 2*(90-theta1)
#Display the results
print("\nResults")
print("Area =", round(area,2))
print("Perimeter =", round(perimeter,2))
print("Angles = ",round(theta1,2),"",round(theta1,2),"",round(theta2,2))
ICS3U Practice Question
Name Your File : “ICS3UslopeIntercept.py”
You have been assigned the task of helping a grade 9 math class with developing equations of linear graphs. Your program needs to all the user to enter the (x,y) coordinates of two points on a cartesian plane and output the equation of the straight line that passes through both of those points. The equation can be displayed in slope-y intercept form
Display the slope and y intercept as both decimals and as fractions. Note you are not allowed to use the built in Fraction function that exists in python. Use variables to represent the numerators and denominators. Don’t worry about converting to lowest terms.
#Inputs from the user
print("Enter first point")
x1 = int(input("x: "))
y1 = int(input("y: "))
print("\nEnter second point")
x2 = int(input("x: "))
y2 = int(input("y: "))
#Calculate slope
mN = y2 - y1
mD = x2 - x1
m = mN/mD
#Calculate y intercept
bN = y1*mD - mN*x1
bD = mD
b = bN/bD
#Print Results
print("\nThe Equation is")
print("y=",round(m,1),"x +",round(b,1))
print("y=",mN,"/",mD,"x +",bN,"/",bD)
