ICS4U – Python Sorting Algorithms
ICS4U Learning Goals
In this ICS4U Grade 12 Computer Science lesson you will be learning how to
- Implement different Sorting Algorithms including
- a Selection Sort Algorithm
- a Bubble Sort Algorithm
- an Insertion Sort Algorithm
- a Quick Sort Algorithm
Sorting
Sorting involves putting the values in the list in either ascending or descending order. There are many different types of sorting algorithms. Some work faster then other for certain scenarios. In this course we will look at a few easy to understand algorithms
For the algorithms below, I’m going to always assume we are sorting in ascending order (smallest to largest)
Make note that with the code I’m providing you the functions modifies the original list that was sent to the function. It does not return a new list leaving the original untouched.
Selection Sort
The idea for a selection sort is pretty straightforward
- First find the smallest element in the list and swap it with the first element
- Now look for the next smallest value in the array and swap it with the second element
- Now look for the third smallest value in the list and swap it with the third element
- Repeat the process over and over until the list has been sorted
Implementation
Make sure to Select “Selection Sort” from the Menu
#a is the list to sort
#This algorithm sorts in ascending order (smallest to biggest)
def selectionSort(a):
small = 0
smallIndex = 0
for i in range (0,len(a)):
#Sets the minimum to the first non sorted location
small = a[i]
#Search the rest of the list for the smallest value
for j in range(i,len(a)):
#Found a new smallest? record its location too.
if a[j] <= small:
small = a[j]
smallIndex = j
#Make the swap
a[smallIndex] = a[i]
a[i] = small
Bubble Sort
The idea for the bubble sort is as follows
- Compare the first two elements in the list and swap if they are not in the correct order
- Compare the next two elements in the list and swap if they are not in the correct order
- Continue this process for all the adjacent elements in the list
- By the time you have cycled through all the values in the list once, the largest value will have been moved to the end of the list and is in the correct position
- Now repeat this “Bubbling” process again using only the still unsorted values in the list
- After every iteration of the list, you will sort one more number into its correct position.
Implementation
Make sure to Select “Bubble Sort” from the Menu
#a is the list to sort
#This algorithm sorts in ascending order (smallest to biggest)
def bubbleSort(a):
#The number of "Bubble Cycles" is the length of the list
for i in range(0,len(a)):
#Cycle through all adjacent elements not yet sorted (reduces each time)
for j in range(1,len(a)-i):
#Check for out of order and swap elements
if a[j-1] > a[j]:
swapValue = a[j]
a[j] = a[j-1]
a[j-1] = swapValue
Insertion Sort
The insertion sort is based on the idea of inserting a new element into an already sorted list
- To start, assume the first element is already sorted in its correct position (even if its not)
- Take the 2nd element out, and find its spot in the already sorted list (in this case the sorted list is only the first element, so compare and swap if necessary)
- Now the two numbers at the start of the list are sorted, take the 3rd element out and find its correct spot in the sorted list
- Now three numbers are sorted at the start of the list so take the 4th element out and find its correct spot in the sorted list
- Repeat until there are no more elements to remove and insert in the correct position.
Implementation
Make sure to Select “Insertion Sort” from the Menu
#a is the list to sort
#This algorithm sorts in ascending order (smallest to biggest)
def insertionSort(a):
#Cycle through all the elements in the list 1 -> end (Assume 0 index is sorted)
for i in range(1,len(a)):
#Take a value out of the list to insert in the already sorted list
insertValue = a[i]
#Find the correct spot in the already sorted list
location = i
while location > 0 and a[location - 1] > insertValue:
a[location] = a[location - 1]
location = location - 1
#Now have found insertValue's location so insert it
a[location] = insertValue
Quick Sort
The quick sort is much faster then the previous 3 sorting algorithms, but much more complicated to implement and understand. Its a recursive algorithm. It is similar to an insertion sort in the sense that it inserts items into the list in their correct position after each pass through of the data
Consider a list that is already sorted in ascending order. We can pick any value in the list, K, and we know that all values less than K are to the left, and all values greater than K will be to the right
Quick sort uses this concept and applies it to the unsorted list. Each pass of quicksort chooses a value for K from the unsorted list to be inserted into its correct location. This element is called a pivot. The pass then rearranges all other elements so they are either to the left or the right of the pivot. All of theses other values will still be out of order but the pivot value will now be in its final position. This rearrangement is called a partition of the list. To achieve the partition, you can use two markers to locate values that are on the wrong side of the list, and then send them over to the other side
Consider the list:
First you need to select the pivot value. Any element will work but to keep it simple you can just use the first value in the list. Make a copy of it so it will be easier to swap into its correct position

Next you need a set of variables to track the left and right side of the partition. All elements between these values need to be checked against the pivot. The first time through the partition process your left marker is the first value and the right marker is the last value in the list.

The right maker starts moving toward the center of the list looking for values that should not be on that side. The first value it checks is 87, which is on the correct side, the next value it checks is 37, which is not on the correct side. It is moved to the location of the left marker.

Now the left marker will move toward the center. Both the values 46 and 12 are less than 61 and on are the correct side, but 63 is not so it is moved to the location of the right marker.

The process now resumes from the right marker. The active marker will always switch after a swap occurs
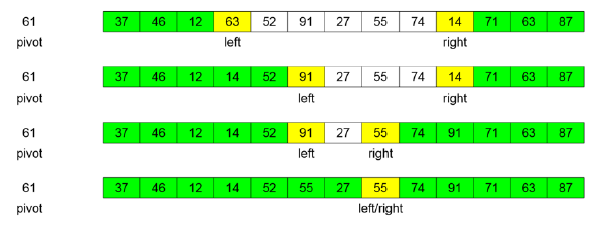
In the final movement the left marker moves toward the center and ends up at the same location as the right marker. No further swaps are required and that location is proper location in the list for the pivot.

This process can now be repeated for each sub list to the right and left of the pivot. This could be accomplished using recursion. For each sub list you pick the left most item for the pivot.
The sort continues with each partition until there is only one element left in that partition
Implementation
Make sure to Select “Quick Sort” from the Menu (Might be easier to watch if you increase the size of the data set in the simulation) ->Yellow Box Bottom Left Corner. I suggest about 15
def quickSort(a):
sortPartition(a,0,len(a)-1)
def sortPartition(a,low,high):
if low < high:
#Set Markers
left = low
right = high
#Pick Pivot
pivot = a[low]
#Set Active Marker
active = "R"
#Partition the list
while left < right:
#Right marker action
if active == "R":
#Move right marker left until it finds a value on the wrong side
while a[right] >= pivot and left < right:
right = right - 1
#Move value that is on the wrong side
a[left] = a[right]
#Make other side active
active = "L"
if active == "L":
#Move left marker until it finds a value on the wrong side
while a[left] <= pivot and left < right:
left = left + 1
#Move value that is on the wrong side
a[right] = a[left]
#Make other side active
active = "R"
#Put pivot in the correct position
a[left] = pivot
#Recursive sort the left partition
sortPartition(a,low,left-1)
#Recursive sort the right partition
sortPartition(a,right + 1, high)
Note, you will notice there are two functions here. The first is just so you can call the sort by just sending the list, so you don’t have to think about sending the high and low index values from the main function
Built In Sort
Python lists have a sorting function built directly into them. It is called a Tim Sort (named after one of the python developers)
list = [3,4,6,6,9,1,3,2,1,8,4,3,9]
#Modifies the original list to be sorted in ascending order
list.sort()
print(list)
list = [3,4,6,6,9,1,3,2,1,8,4,3,9]
#Modifies the original list to be sorted in descending order
list.sort(reverse = True)
print(list)
ICS4U Coding Questions
Try to code the following questions using an IDE of your choice. You will save those files on your computer for future reference.
Each question has:
- A video of your teacher live coding and explaining the solution
- The final code used in the video.
Try your best to solve the problems yourself without looking at the solutions.
Make sure you test your programs with multiple different inputs to ensure it is functioning properly.
Treat these questions like Math homework (Do as many as you feel you need to do to feel comfortable with the material)
ICS4U Practice Question
Name Your File: “ICS4UnewListSort.py”
Modify the selection sort algorithm so that instead of modifying the original list, it returns a new sorted list and leaves the original list passed to it untouched.
Make sure to create a test program that checks to see if your function works by printing out both the new sorted list and the original list after the sort function has been run
import random
def selectionSort(original):
#Make a copy of the list to sort
a = []
for i in range(0, len(original)):
a.append(original[i])
small = 0
smallIndex = 0
for i in range (0,len(a)):
#Sets the minimum to the first non sorted location
small = a[i]
#Search the rest of the list for the smallest value
for j in range(i,len(a)):
#Found a new smallest? record its location too.
if a[j] <= small:
small = a[j]
smallIndex = j
#Make the swap
a[smallIndex] = a[i]
a[i] = small
#return the copy
return a
def main():
#Generate a random list
myList = []
for i in range(0, 10):
myList.append(random.randint(0, 20))
sortedList = selectionSort(myList)
print(myList)
print(sortedList)
main()
ICS4U Practice Question
Name Your File: “ICS4UfindMedian.py”
Take a list of numbers and find the median.
- The median is the middle number in an ordered list
- If the list has an even # of elements, then the median is the average of the two middle values
import random
#Generate a random list
N = random.randint(1,15)
myList = []
for i in range(0, N):
myList.append(random.randint(0, 20))
#Order the list
myList.sort()
#Find the median
if len(myList) % 2 != 0:
median = myList[len(myList)//2]
else:
median = ( myList[len(myList)//2] + myList[len(myList)//2-1] ) / 2
#Display list and the median
print(myList)
print(median)
ICS4U Practice Question
Name Your File: “ICS4UradixSort.py”
In the lesson, you were looking at visual representations of a few sorting algorithms on the website
One of the sorts, we didn’t discuss was the Radix Sort
Its pretty straightforward to see what its doing. I want you to write a function that implements that algorithm.
- Use a 2D list to implement the digit “buckets”.
- Each row of that list can represent each digit from 0 – 9
def radixSort(a):
# Create Buckets (1 bucket for each digit) -> Row index# of 2D list matches the digit
buckets = []
for i in range(0, 10):
buckets.append([])
# Need the number with the maximum number of digits to determine how many sweeps of the list
maxNum = max(a)
maxDigits = len(str(maxNum))
# Sort the list
for d in range(0, maxDigits):
# Take from the list and put into the buckets
for i in range(0, len(a)):
number = a[i]
currentDigit = number // 10 ** d % 10
buckets[currentDigit].append(number)
a.clear()
# Take From the buckets and put back into the list
for i in range(0, len(buckets)):
digit = buckets[i]
for j in range(0, len(digit)):
number = digit[j]
a.append(number)
digit.clear()
#Testing
import random
def main():
# Generate a random list
myList = []
for i in range(0, 20):
myList.append(random.randint(0, 100000))
#myList = [7055, 847, 3531, 1943, 8297, 182, 28, 1812, 2861, 5608]
radixSort(myList)
print(myList)
main()
