ICS4U – Recursion in Python

ICS4U Grade 12 Computer Science ICS4U – Recursion in Python

ICS4U Learning Goals

In this ICS4U Grade 12 Computer Science lesson you will be learning how to

Define problems recursively
Implement some straightforward recursive algorithms

What is Recursion?

You are used to programming and solving problems using control structures such as if-else statements (selection structures) and iterative loops (repetition structures)

Another control mechanism that can be used in problem solving and programming is recursion

The basic idea behind recursion is this:

If the problem is considered easy solvable, solve it immediately
If the problem can’t be solved immediately, divide it into easier problems, then solve the
easier problems

Generally when a problem can be defined in terms of itself then it can be solved recursively

Triangle Numbers

The total number of pins in a triangular arrangement is called a triangle number.

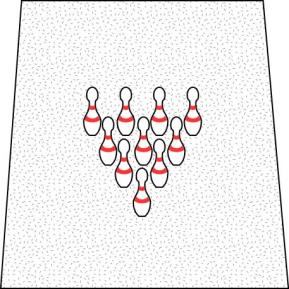
You can expand that pattern by keep adding rows with more pins

Row 1 -> 1 Pin
Row 2 -> 3 Pins
Row 3 -> 6 Pins
Row 4 -> 10 Pins
Row 5 -> 15 Pins
Row 6 -> 21 Pins
Row 7 -> 28 Pins

There is a pattern here:

Total # pins in row 1 = 1
Total # pins in row 2 = 2 + Total # of pins in row 1
Total # pins in row 3 = 3 + Total # of pins in row 2
Total # of pins in row 4 = 4 + Total # of pins in row 3
Total # of pins in row 5 = 5 + Total # of pins in row 4

Mathematically you can write out the # of pins in the Nth row as

Triangle (N) = N + Triangle (N – 1)

Triangle(3)

= 3 + Triangle(2)
= 3 + (2+Triangle(1))
= 3 + (2 + (1))
= 6

Triangle (7)

= 7 + Triangle(6)
= 7 + (6 + Triangle(5))
= 7 + (6 + (5 + Triangle(4)))
= 7 + (6 + (5 + (4 + Triangle(3))))
= 7 + (6 + (5 + (4 + (3 + Triangle(2)))))
= 7 + (6 + (5 + (4 + (3 + (2 + Triangle(1))))))
= 7 + (6 + (5 + (4 + (3 + (2 + 1)))))
= 28

Because you have defined the Nth Triangle number in terms of itself, this is a perfect problem to solve recursively.

Notice that in both examples above the sequence of additions ended with Triangle(1) = 1. This is called the base case for the problem

A base case is a problem that can be easily solved immediately
It typically tells you when the recursion should stop

If you were to translate this into code you would have the following

				
					
def triangle(N):
    
    #Base Case
    if N == 1:
        return 1
    
    #Recursive Call
    else:
        return N + triangle(N-1)

Notice that the Tell Tale Sign of a Recursive Function call in programming is that you define a function that calls itself

ICS4U Interactive Learning Activity - Grade 12 Computer Science

Write a main program for the Triangle Function defined above and test to see if you are getting the correct results

Try multiple different values of N
Try printing the value of N inside the function, and you will see the sequence of calls printed out

Go to the following website and watch how the function works its way through until the base case is hit and the recursion stops.

When you see a pink box, you can click on it to interact and watch the function calls
You might notice that the website talks about Java, but the explanation is good and its pretty much the same anyways.

Python Editor

Solution

				
					
def triangle(N):

    if N == 1:
        return 1
    else:
        return N + triangle(N-1)

def main():
    num = int(input("Calculate Triangle Number for N = "))

    tNumber = triangle(num)

    print("Triangle(",num,") = ", tNumber)

main()

Fibonacci Sequence

You have probably studied and are familiar with the Fibonacci Sequence of numbers

1,1,2,3,5,8,13,,21,34,55,….

Each value in the sequence is found by adding the previous two values in the sequence.

Mathematically we can define this as

Fib (N) = Fib(N-1) + Fib(N-2) for N >= 3

The base cases for this recursion are Fib(1) = 1 and Fib(2) = 1

Translating that into a python function would look as follows

				
					
def fib(N):

    if N == 1 or N == 2:
        return 1
    else:
        return fib(N-1) + fib(N-2)

ICS4U Interactive Learning Activity - Grade 12 Computer Science

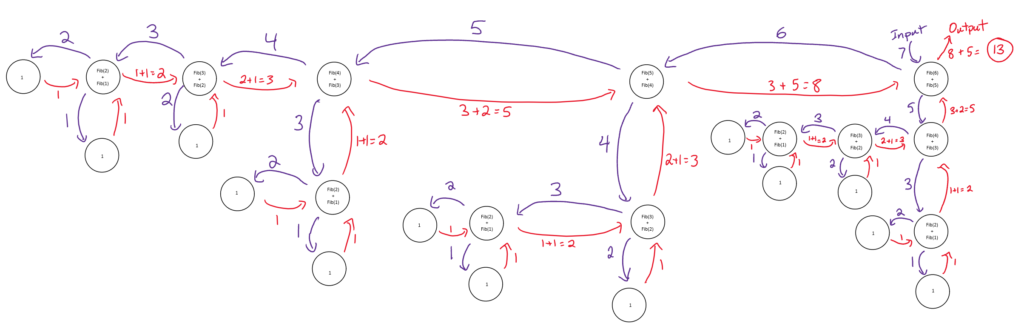
Look at the following recursive activation diagram for trying to find the 5th Fibonacci number

Purple arrows are the values being sent to the function
Red arrows are the values returned from the function

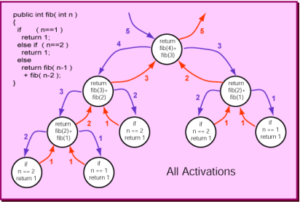
You can trace through the activations of the recursive calls here
Try to draw the activation for the 7th fibonacci Number

Solution

Iteration vs Recursion

You might be wondering, why recursion is necessary at all, when the two programs above could have easily been written with a loop.

Iterative Triangle Number

If you look at the pattern that occurs for the Nth triangle number, you will see that its value is just the sum of the numbers from 1 to 10

Triangle(3) = 6 = 1 + 2 + 3
Triangle(7) = 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7

That is easily accomplished using a simple loop

				
					
def triangle(N):
    sum = 0
    for i in range(1,N):
        sum = sum + i
    return sum

Iterative Fibonacci Sequence

This one might be a little more complicated to understand from a looping perspective, but just need to keep track of the previous two values in some variables.

				
					
def fib(N):

    f1 = 1
    f2 = 1
    for i in range(1,N-1):
        nextValue = f1 + f2
        f1 = f2
        f2 = nextValue

    return f2

Well, the answer to the above question of recursion vs iteration, isn’t exactly straight forward.

Generally Speaking

Code size is smaller and sometimes logically easier to understand using recursion
Iterative solutions are usually faster (It takes more time to call functions then to execute a loop)
Recursion can take up more memory and is subject to Stack Overflow Errors
Some problems are just naturally recursive in nature
- Towers of Hanoi
- Maze Solving
- Sorting Methods

ICS4U Interactive Learning Activity - Grade 12 Computer Science

Comparing Execution Times - Triangle Numbers

Run the Following Code to compare the execution times for the iterative vs the recursive Triangle Number Algorithms

Try a small number < 10
Try a number between 10 and 100
Try a number over 1000000

				
					
import timeit

def triangleRecursive(N):

    if N == 1:
        return 1
    else:
        return N + triangleRecursive(N-1)

def triangleIterative(N):
    sum = 0
    for i in range(1,N+1):
        sum = sum + i
    return sum

def main():
    num = int(input("Calculate Triangle Number for N = "))

    print("\nRecursive:")
    start = timeit.default_timer()
    tNumber = triangleRecursive(num)
    end = timeit.default_timer()
    elapsedNS = round((end - start)*10**9)
    print("Triangle(",num,") = ", tNumber)
    print("Solution took",elapsedNS,"nanoseconds\n")

    print("Iterative:")
    start = timeit.default_timer()
    tNumber = triangleIterative(num)
    end = timeit.default_timer()
    elapsedNS = round((end - start) * 10 ** 9)
    print("Triangle(", num, ") = ", tNumber)
    print("Solution took",elapsedNS,"nanoseconds")

main()

Python Editor

Comparing Execution Times - Fibonacci Numbers

Run the Following Code to compare the execution times for the iterative vs the recursive Fibonacci Number Algorithms

Try a small number < 10
Try 35
Try 40 -> Be patient, very very very patient…..
Try a number over 1000000

				
					
import timeit

def fibRecursive(N):

    if N == 1 or N == 2:
        return 1
    else:
        return fibRecursive(N-1) + fibRecursive(N-2)

def fibIterative(N):

    f1 = 1
    f2 = 1
    for i in range(1,N-1):
        nextValue = f1 + f2
        f1 = f2
        f2 = nextValue

    return f2

def main():
    num = int(input("Calculate the Fibonacci Number for N = "))

    print("\nRecursive:")
    start = timeit.default_timer()
    fNumber = fibRecursive(num)
    end = timeit.default_timer()
    elapsedNS = round((end - start)*10**9)
    print("Fibonacci(",num,") = ", fNumber)
    print("Solution took",elapsedNS,"nanoseconds\n")

    print("Iterative:")
    start = timeit.default_timer()
    fNumber = fibIterative(num)
    end = timeit.default_timer()
    elapsedNS = round((end - start) * 10 ** 9)
    print("Fibonacci(", num, ") = ", fNumber)
    print("Solution took",elapsedNS,"nanoseconds")

main()

Python Editor

Python Stack and Overflow Errors

You will learn in the next unit about a data structure called a Stack, but when python makes function calls, that structure is used to store the set of new local variables and parameters each time the function is called. There is only so much space that is available on that stack, and as we have seen, the amount of function calls that a recursive solution can make can become very high.

In the previous learning activity you probably noticed that you were getting a Recursion Depth Exceeded error. This is a stack overflow error where there are too many functions calls and the stack wouldn’t have enough space to handle that many.

Iterative vs Recursive GCD

The greatest common divisor (GCD) algorithm is another common algorithm that can be written both recursively and iteratively. It finds the largest factor that exists between 2 numbers (a,b)

You can see the simplicity of the recursive code vs the iterative version

				
					
def gcd(a,b):
    if a == 0:
        return b
    else:
        return gcd(b % a , a)

				
					
def gcd(a, b):
    # Largest divisor 1 -> if no other ones found
    g = 1

    # start search for divisors at the smallest number
    if a > b:
        start = b
    else:
        start = a

    # Count backwards to find the largest divisor
    for i in range(start, 1, -1):

        # Found largest divisor so stop
        if a % i == 0 and b % i == 0:
            g = i
            break

    return g

Towers of Hanoi

The Towers of Hanoi Problem is a traditional mathematical problem that can be solved using recursion. Watch the video and see if you can understand the algorithm. The code it gives is not in Python, but see if you can simulate this puzzle yourself in Python if you have time, but I’m more concerned with you just getting familiar on how this could be solved recursively

Counting

Here is an example of a recursive function that counts up by 3 for N number of times.

				
					
def count3(N):

    if N == 0:
        return 0
    else:
        return 3 + count3(N-1)

def main():

    #Counts up by 3 5 times, so prints 15
    print(count3(5))

    #Counts up by 3 20 times, so prints 60
    print(count3(20))

main()

The recursion is acting like a loop in this case, executing N number of times and adding 3 each time the recursive function is called

ICS4U Coding Questions

Try to code the following questions using an IDE of your choice. You will save those files on your computer for future reference.

Each question has:

A video of your teacher live coding and explaining the solution
The final code used in the video.

Try your best to solve the problems yourself without looking at the solutions.

Make sure you test your programs with multiple different inputs to ensure it is functioning properly.

Treat these questions like Math homework (Do as many as you feel you need to do to feel comfortable with the material)

ICS4U Practice Question

Name Your File: “ICS4Ufactorial.py”

Write a recursive solution to calculating a factorial. The factorial of a number N is the product of all the numbers from 1 to N. Mathematically a factorial is written as N!

5! = 5 x 4 x 3 x 2 x 1
6 ! = 6 x 5 x 4 x 3 x 2 x 1
7! = 7 x 6 x 5 x 4 x 3 x 2 x 1

This definition is recursive because the Nth factorial is N multiplied by the N-1 factorial

Factorial(N) = N * Factorial(N-1)
By definition in math the factorial of zero is 1 (That is the base case)

Solution

				
					
def factorial(N):

    if N == 0:
        return 1
    else:
        return N * factorial(N-1)

ICS4U Practice Question

Name Your File: “ICS4Usquared.py”

In this question you are going to write a recursive function for implementing the Square of a Number 𝑁².

An interesting way to compute the square of a number is to use the fact that

(N-1)² = N² – 2N + 1

which would mean that

N² = (N-1)² + 2N – 1

Solution

				
					
def squared(N):

    if N == 1:
        return 1
    else:
        return squared(N-1) + 2 * N - 1

ICS4U Practice Question

Name Your File: “ICS4UpyramidalNumbers.py”

Let’s take a look at a tetrahedron made up of tennis balls.

Start with a triangular arrangement of tennis balls for the bottom layer (Each side of the triangle has the same number of tennis balls)
Next Stack up tennis balls a layer at a time until there is only 1 ball at the top of the pyramid

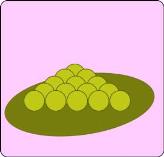
The Nth pyramidal number is the total number of balls in a pyramid that has a base side length of N tennis balls

You can solve this problem by adding up the number of balls in each layer (which just happen to be the Triangle Numbers from the lesson)

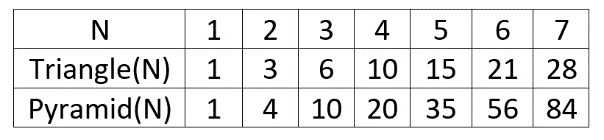
Notice that the Nth pyramidal number is just the Nth Triangle Number plus the pervious Pyramidal Number

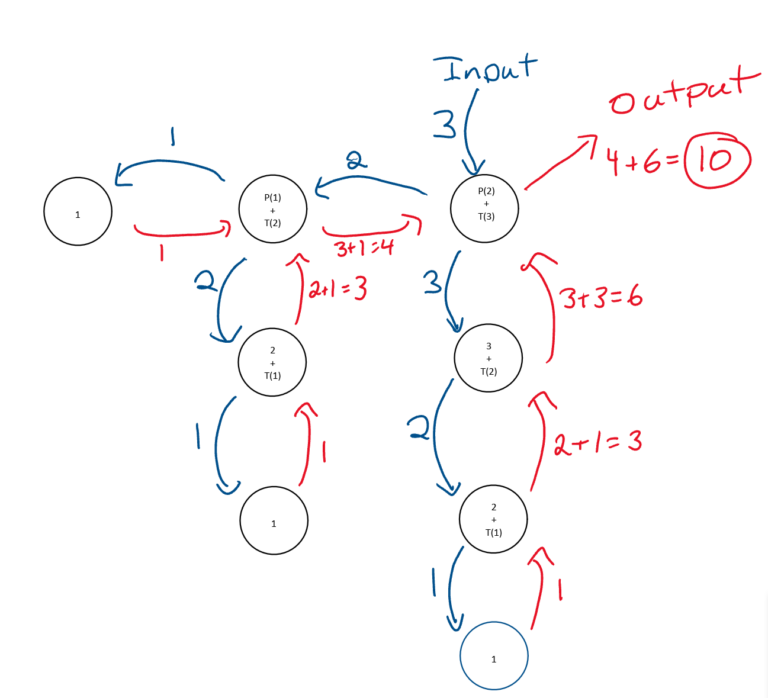
Write a recursive function to find Pyramidal Number and draw the activation diagrams showing the recursive calls for N = 3

Solution

				
					def triangle(N):

    if N == 1:
        return 1
    else:
        return N + triangle(N-1)

def pyramidal(N):

    if N == 1:
        return 1
    else:
        return pyramidal(N-1) + triangle(N)

def main():

    num = int(input("Enter N: "))
    print(pyramidal(num))

main()

ICS4U Practice Question

Name Your File: “ICS4UsumOfList.py”

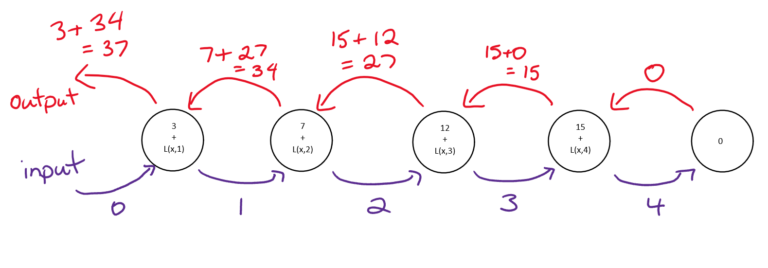
It is possible to write an algorithm that finds the sum of the values inside a list using recursion as well

sumList(theList,index) = theList[index] + sumList(theList, index + 1)

The base case is when the index is equal the length of theList and the recursive function should return 0

Write the function to implement this sum recursively

test it out with different lists

Draw the activation diagram showing the recursive calls for the following list

[3,7,12,15]

Solution

				
					
def sumList(theList,index):

    if index == len(theList):
        return 0
    else:
        return theList[index] + sumList(theList, index + 1)


def main():

    x = [1,2,3,4,5]
    print(sumList(x,0))

    x = [4,3,7,12,17,20,22]
    print(sumList(x, 0))


main()

Return to ICS4U Main Page

Previous Lesson

Back to Course

Next Lesson